搜索结果: 1-15 共查到“动力系统”相关记录18条 . 查询时间(2.437 秒)
Part of the motivation of this paper comes from the recent paper [W. Guo and H.-Z. Zhou, SIAM J. Control Optim., 57 (2019), pp. 1890–1928], where an adaptive control approach was used to estimate in r...
雅各布·帕里斯（Jacob Palis），巴西国籍，数学家。1940年 3月生于巴西。1967年获得美国加州大学伯克利分校博士学位。1970年当选为巴西国家科学院院士。
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars：Convergence of the Planewave Approximations for Incommensurate Systems
不可测系统 平面波逼近 收敛性
2023/12/11
Incommensurate structures come from stacking the single layers of low-dimensional materials on top of one another with misalignment such as a twist in orientation. While these structures are of signif...
带有固执个体的级联观点动力学的同步研究
固执个体 级联观点 动力学 同步研究
2023/12/13
This article investigates a two-timescale opinion dynamics model, named the concatenated Friedkin–Johnsen (FJ) model, which describes the evolution of the opinions of a group of agents over a sequence...
中国科学院合肥物质科学研究院专利：一种电子驻车制动系统的电源模块
中国科学院合肥物质科学研究院 专利 电子驻车 制动系统 电源模块
2023/9/14
中国科学院合肥物质科学研究院专利：一种电子驻车制动系统的电源模块
北京大学110周年庆·数学学人 | 文兰：优美深邃的微分动力系统（图）
文兰 北大 数学 微分动力系统
2023/6/16
2023年，北京大学数学学科迎来成立110周年，百十年经风雨而续薪火，再回首忆往昔而向未来。站在这个有着特别意义的节点上，我们推出了“110周年庆系列文章”栏目，以人物专访、回忆征稿等形式，回望北大数学学人一路走来的足迹以及学科发展历程。
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars： Derivation of the Vlasov equation from quantum many-body Fermionic systems with singular interaction
奇异相互作用 量子多体 费米子系统 弗拉索夫方程
2023/5/12
We consider the combined mean-field and semiclassical limit for a system of the N fermions interacting through singular potentials. We prove the uniformly in the Planck constant h propagation of quant...
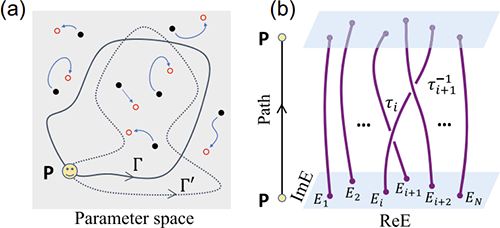
非厄米多带系统中例外简并的非阿贝尔拓扑（图）
非厄米多带系统 简并 非阿贝尔拓扑
2023/4/24
非厄米体系在过去几年受到理论和实验学家的广泛关注，其相关物理性质的研究仍在蓬勃发展。较于厄米哈密顿量描述的体系，非厄米系统拥有例外点/线（Exceptional point/line）、趋肤效应等独有特征。其中例外点是一种与Dirac点和Weyl点完全不同的能级简并点。在例外点处，简并的本征能量一般呈现分数型色散关系且对应的本征波函数合并（coalescence）。非厄米例外点在很多有趣的现象或功...
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars：Ergodic Theory and Semisimple Groups
遍历理论 半简单群 马古利斯超刚性定理
2023/4/13
We go through Zimmer's book Chapter 2-3, making some preparations for Margulis super-rigidity theorem.
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars：A deformation of Borel equivariant homotopy
博雷尔等变 同伦变形 R-动力稳定
2023/4/18
The R-motivic stable homotopy category has a close connection to the C2-equivariant category via the C2-equivariant Betti realization map.
For the bigraded homotopy groups, the C2-equivariant spectra...
质点-弹簧-惯容系统的特征值反问题（李婵颖、谢奇达）
质点-弹簧-惯容系统 特征值 反问题
2023/2/22
彻底解决了质点-弹簧-惯容振动系统的特征值反问题。在结构动力学中，时常需要针对给定的频谱数据来设计系统的物理参数，这类问题可转化为相应系统的特征值反问题。当振动系统引入惯容，则可实现传统质点-弹簧振动系统所不具备的多重固有频率情形。但多重固有频率的配置问题相对复杂。我们引入构造性设计方法，给出了质点-弹簧-惯容振动系统实现其固有频率任意配置（可包括重根情形）的充分必要条件，该条件由给定特征值重数及...
Academy of Mathematics and Systems Science, CAS Colloquia & Seminars： A decoupled, linear, and unconditionally energy stable finite element method for a two-phase ferrohydrodynamics model
两相铁流体 动力学模型 能量稳定 有限元方法
2023/4/28
In this talk, we present numerical approximations of a phase-field model for two-phase ferrofluids, which consists of the Navier-Stokes equations, the Cahn-Hilliard equation, the magnetostatic equatio...
中国科学院数学物理学部龙以明院士（图）
中国科学院数学物理学部 哈密尔顿动力系统 龙以明 院士
2022/9/8
数学家，长期从事哈密尔顿动力系统以及辛几何有关问题研究。1948年10月生于重庆市。1973年毕业于天津师范学院（现天津师范大学），1981年于南开大学获硕士学位，1987年于美国威斯康星大学(Madison)获博士学位。2007年当选为中国科学院院士。
中国科学院数学物理学部郭柏灵院士（图）
中国科学院数学物理学部 非线性发展方程 无穷维动力系统 郭柏灵 院士
2022/9/8
数学家，主要从事非线性发展方程及其无穷维动力系统研究。1936年10月生于福建龙岩。1958年毕业于复旦大学数学系。2001年当选为中国科学院院士。
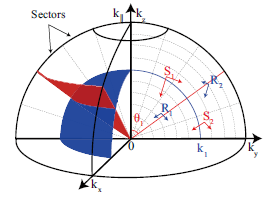
螺旋旋转湍流中能量/螺旋度联合输运机制研究新进展（图）
螺旋旋转湍流 能量/螺旋度 联合输运机制
2023/1/7
螺旋度作为三维湍流中唯一的具有手性的二阶无粘不变量，是湍流拓扑结构的定量表征，在湍流的演化中扮演着重要角色。自然界的旋转流动经常伴随着高的螺旋度，旋转与螺旋度的耦合效应在叶轮机械等工业领域具有重要的研究及应用价值。